Pro nemálo aplikací potřebujeme jako vstup nějaká náhodná čísla, ať se jedná o simulace všeho možného, kryptografii, statistiku, numerické integrování nebo pro hry. K tomu používáme tzv. generátory náhodných čísel (angl. random number generator – RNG). Předpokladem je, že vygenerovaná náhodná čísla jsou opravdu náhodná a není tam nějaký skrytý vzorec.

A to je problém. Většinou potřebujeme náhodná čísla v počítači a většina programovacích jazyků k tomu má příslušné funkce. Ale jsou ta náhodná čísla opravdu náhodná? V principu ne. Samotný digitální počítač je deterministický a náhoda tam nemá co dělat, naopak je nežádoucí. Proto se musejí generovat náhodná čísla poměrně sofistikovaně. V takovém případě mluvíme o tzv. pseudo-náhodných číslech.

Naopak, například v případě kryptografie dokonce využíváme toho, že náhodná čísla vlastně nejsou tak náhodná. Prakticky všechny generátory potřebují tzv. seed, tedy nějaké počáteční (ideálně náhodné) číslo od kterého se algoritmus tzv. odpíchne. Tedy, pokud generátoru dáme opět stejný seed, bude generovat zase stejná čísla. V kryptografii právě takové číslo, které tvoří seed může tvořit tajné heslo k šifrování/dešifrování.

Často však chceme pokaždé jiná čísla, proto se často bere například současný čas na setiny sekundy přesně jako takový seed.

Mimo počítačový svět je to jednodušší. Můžeme použít něco, co se složitě spočítá. Například 49 koulí v barelu, když se losuje Sportka. Jedná se v podstatě stále o deterministickou fyziku, a teoreticky, pokud sestavíme příslušné pohybové rovnice a zadáme veškeré počáteční podmínky, tak lze spočítat, co vypadne. Ale co opravdu je náhodný z principu je cokoliv, kde přistupuje k objektům na mikroskopické úrovni, kde funguje kvantová fyzika. Stačí například detekovat nějaké radioaktivní záření (včetně kosmického) abychom dostali opravdu náhodné číslo.

A tady se dostáváme ke kvantovým počítačům. Zde v principu je získání náhodného čísla přirozené. Podívejme se na kvantový obvod níže. Na začátku máme 0. Poté aplikujeme Hadamardovo hradlo a získáme superpozici 0 a 1, obě se stejnou pravděpodobností 50%. Poté provedeme měření, které nám vrátí 0 nebo 1 se stejnou pravděpodobností naměření.

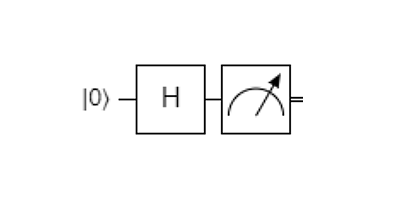
Ale ani tady věc není tak jednoduchá. Popis výše platí pro perfektní qubit. Hodnota 1 je často reprezentováno excitací kvantového systému. Excitace z principu jsou nestabilní a mají tendenci deexcitovat do základního stavu, tedy na nulu. To by mohlo vést k nepatrnému přebytku nul nad jedničkami. Nicméně jedná se o velmi malý kvantový obvod a dnešní excitované stavy jsou dostatečně stabilní, že u některých kvantových systémů to již můžeme zanedbat.

Klasické RNG vs Kvantové RNG

Ale nyní k otázce z nadpisu, opravdu potřebujeme kvantové zařízení na generování náhodných čísel?

Odpověď je ano i ne. Záleží na využití.

Odpověď ne lze aplikovat pro většinu aplikací, jako jsou simulace, numerické integrace atd. Dnes lze implementovat již dostatečně pokročilé funkce pro generování náhodných čísel a s trochu důvtipným seedem dostaneme rozumně náhdná čísla. I když máme nějaké statistické testy, tak jejich výsledek je kompilovaný a nelze udělat kvalitní závěry o náhodnosti. A to je problém, pokud potřebujete nějaký certifikát nebo ověření, že čísla jsou opravdu náhodná.

A tady je první trumf kvantových generátorů, kde lze náhodná čísla certifikovat i verifikovat. To může být vhodné hlavně pro kryptografické účely, kde potřebujete opravdu velmi vysokou úroveň zabezpečení, nebo třeba například pro loterie, aby se nestalo to co v roce 2010, kde jeden šikula dostal malware na počítač, který generoval náhodná čísla pro loterie…

Druhá motivace je spojená s kvantovou distribucí klíče (viz náš seriál), kde v principu máme dva hlavní směry protokolů. Ty založené na E91 generátor náhodných čísel nepotřebují, protože sám proces distribuce klíče klíč náhodně generuje. Avšak u protokolů založených na BB84 (které jsou technicky jednodušší) již generátor náhodných čísel potřebujeme, neboť potřebujeme nejdřív klíč vygenerovat a následně jej poslat. A z matematického hlediska, aby metoda byla opravdu neprolomitelná, tak je potřeba implementovat opravdu kvantový generátor náhodných čísel.

A kde jsou QRNG dnes?

V případě QKD je kvantový generátor náhodných čísel standardní součástí a většina poskytovatelů hardwarového řešení pro QKD nabízí QRNG i jako samostatný modul.

Trochu spíše na hype vlně se vezou mobilní telefony s čipem pro kvantový generátor náhodných čísel. Zde se očekává, že QRNG bude sloužit hlavně k vyšší kryptografické bezpečnosti.

Nejnověji teď IBM a Cambirge Quantum computing oznámili QRNG jako cloudovou službu. Která navíc přidává i tu zásadní výhodu popsanou výše, tedy certifikaci a ověření. V tomto směru se jedná o první generátor opravdu náhodných čísel, které lze ověřit a tedy i certifikovat.

Pro ty z vás, které zajímají detaily, tak k ověření se používá Bellův test a využívá se knihovny qiskit_rng.

Závěrem můžeme říci, že QRNG určitě má své místo v kvantové distribuci klíče a pro kryptografii, kde potřebujeme zabezpečení na hodně vysoké úrovni. Také lze očekávat, že některé služby QRNG využijí, ale jen u málo z nich to bude mít opravdu smysl (např. loterie), u ostatních půjde hlavně o PR. Ostatně, v mnoha případech nám stále postačí klasické pseudo-náhodné generátory náhodných čísel.

Avšak, v budoucnu, kdy QRNG čipy budou součástí klasických počítačů (to nastane rozhodně dříve, než budeme mít doma kvantové počítače, pokud vůbec), tak alespoň odpadnou všechny ty neurčitosti quasi-RNG, jako je seed, různé implementace, atd. a obecně to zvýší kybernetockou bezpečnost.